Long term debt funds invest in bonds with very long expiry periods. This period can be as long as 10 years. Most of the long term debt fund investment goes into government bonds.
Holdings of one of the famous long term debt fund : ICICI pru long term fund : http://www.moneycontrol.com/mutual-funds/icici-prudential-long-term-plan-direct-plan/portfolio-holdings/MPI2285
Long term debt fund can go up and down depending upon the yields of these bonds.
The net asset value of any long term debt fund will fall when yield of these 10 year government bond rise. These bonds are traded in bond market and can rise and fall due to variety of reasons:
1) Market sentiments: If inflation is rising or macro data are not coming out good. These bonds will grow attract higher yield and as a result your long term debt fund NAV will fall.
2) RBI policy: Any hike in monetary ratios(repo rate etc) will again increase the yield of 10 year bond yield and decrease ong term debt fund NAV.
To check the present and past yield of 10 year bond refer : https://www.bloomberg.com/quote/GIND10YR:IND
Zenith
Saturday, May 26, 2018
Lessons from "Rich Dad Poor Dad"
I recently finished reading "Rich Dad Poor Dad" by Robert Kiyosaki.
It is a great book to read if you are a teenager or just starting your career.
Robert emphasized on following life principles in his book :
1) Don't blame your employer/job for your miseries. The problem as well as the solution lies within you.
2) Always focus on learning new skills.
3) Money is not that important initially in your career, learning is.
4) Always focus on building assets. Get the assets which can generate cashflow for you.
5) Rich people get richer because their money works for them. Poor people work for money.
6) Invest Invest Invest.
7) A stable job will not make you rich. You get rich by investing in income generating assets.
8) Save yourself from income tax whenever possible.
9) Always keep your accountant/broker/lawyer happy.
10) Surround yourself with intelligent people.
11) Keep on learning throughout your life.
It is a great book to read if you are a teenager or just starting your career.
Robert emphasized on following life principles in his book :
1) Don't blame your employer/job for your miseries. The problem as well as the solution lies within you.
2) Always focus on learning new skills.
3) Money is not that important initially in your career, learning is.
4) Always focus on building assets. Get the assets which can generate cashflow for you.
5) Rich people get richer because their money works for them. Poor people work for money.
6) Invest Invest Invest.
7) A stable job will not make you rich. You get rich by investing in income generating assets.
8) Save yourself from income tax whenever possible.
9) Always keep your accountant/broker/lawyer happy.
10) Surround yourself with intelligent people.
11) Keep on learning throughout your life.
Saturday, May 19, 2018
HOW TO REPLY FOR INCOME TAX NOTICE U/S 143(1)(a).
HOW TO REPLY FOR INCOME TAX NOTICE U/S 143(1)(a).
Your return for AY 2017-18 bearing Ack. No. xxxxxxxxxx was taken up for processing and on verification it was found that it contains arithmetical errors/ incorrect claims/ inconsistencies with respect to Audit Report /Form 26AS and the same is indicated in the table annexed.
2. You are required to provide your response to this communication by electronic mode using your account on the e-filing website, wherein a link has been enabled showing the pending actions. If you agree with the differences indicated in the table annexed, a) either fully, or b) partially,
You may exercise your option of filing a revised return, so that the omissions in the return of income can be completely taken care of within the meaning of section 139(5).
3. However, you have also been afforded a facility in the e-filing portal to state the extent to which you are in agreement with the difference as indicated in the table. For the disagreed portion, please provide the amount and the reason for such disagreement.
Then do not worry here is a simple step by step process to reply for this kind of notice.
2. Click on e-Proceedings:
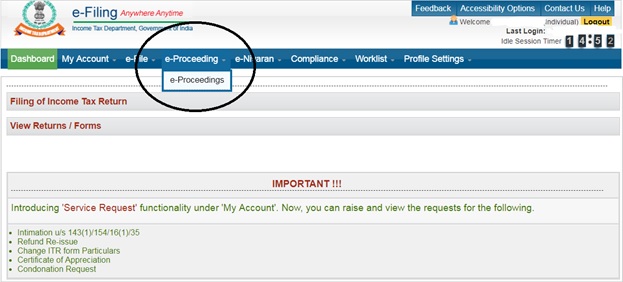
3. Click on proceeding name :
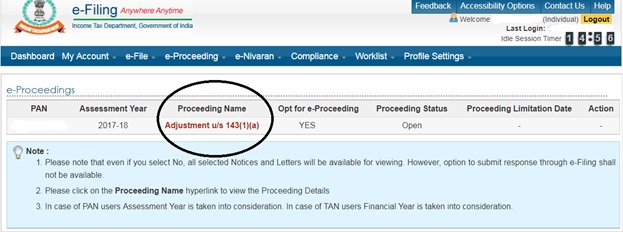
4. Click
on Submit link under Response header:
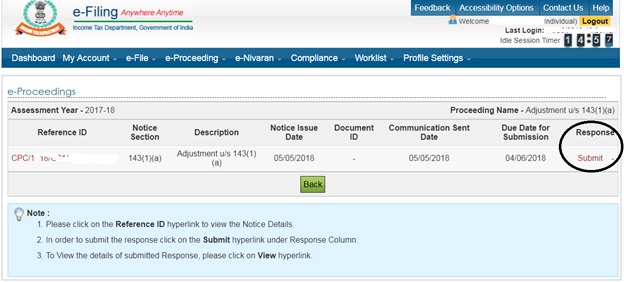
5. You will get 3 options “Agree”/”Partially Agree”/”Disagree”:
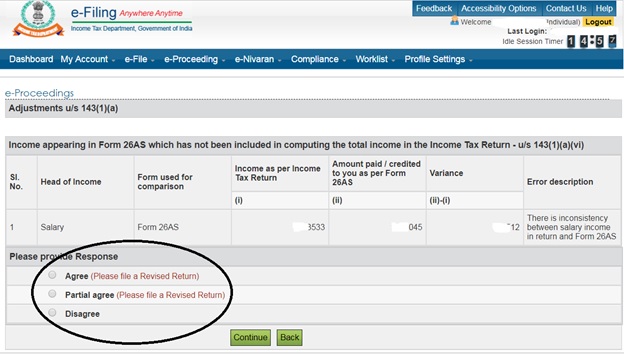
6. If you click “Agree”/”Partially Agree” you will
have to file revised ITR and give acknowledgement number here.
7. If you click “disagree” you are given below
form:
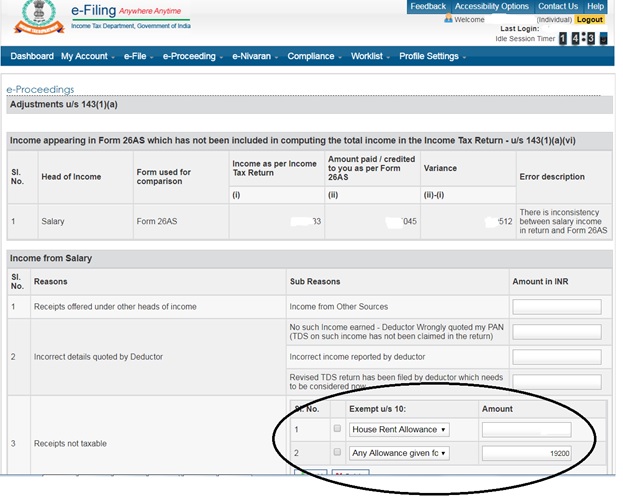
8. Enter
the reason and amount for discrepancy:
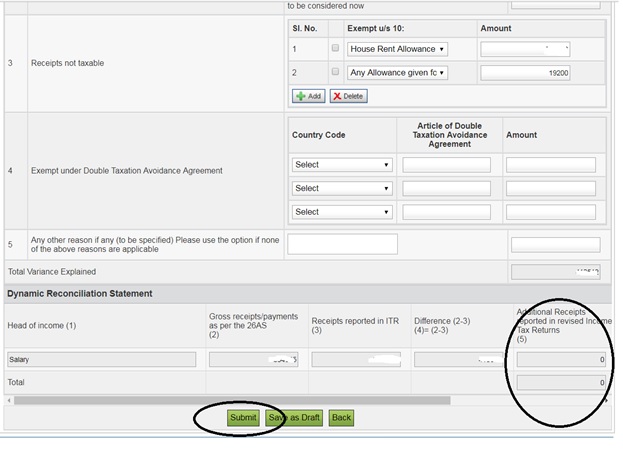
9. Make sure net tax payable is 0 else you have to
file revised ITR. Click Submit.
Saturday, February 3, 2018
How to reach Lansdowne from Delhi
Lansdowne is one of the closest hill station from Delhi.
You can reach Lansdowne by train or road. I personally took train.
1) Take train from Old Delhi railway station to Kotdwar Station. (A/C chair coach costs 375Rs only).
2) From Kotdwar take shared taxi or personal taxi. Shared taxi take 70Rs per passenger and personal reserved taxi takes 700 to 800Rs.
Lansdowne is about 250 Km from Delhi and roads are in good condition. So many people prefer taking their own car there.
You can reach Lansdowne by train or road. I personally took train.
1) Take train from Old Delhi railway station to Kotdwar Station. (A/C chair coach costs 375Rs only).
2) From Kotdwar take shared taxi or personal taxi. Shared taxi take 70Rs per passenger and personal reserved taxi takes 700 to 800Rs.
Lansdowne is about 250 Km from Delhi and roads are in good condition. So many people prefer taking their own car there.
Helpful sites while publishing android apps
Here are the list of sites I usually refer while publishing apps on play store :
1) Design your app icon : https://romannurik.github.io/AndroidAssetStudio/
2) Design your app feature graphic : https://www.norio.be/android-feature-graphic-generator/
3) Step by step guide to publish application :
https://developer.android.com/studio/publish/preparing.html
1) Design your app icon : https://romannurik.github.io/AndroidAssetStudio/
2) Design your app feature graphic : https://www.norio.be/android-feature-graphic-generator/
3) Step by step guide to publish application :
https://developer.android.com/studio/publish/preparing.html
Thursday, February 1, 2018
How to save long term capital gain after budget 2018
Fwd:
Long Term Capital Gains Tax – FAQs
1. What is the budget proposal on LTCG for equities?
Ans – So far, any LT Capital gains made on equities on Exchanges was exempt. The Govt has now proposed an 10% LTCG tax on gains made above Rs 1 Lakh
2. When is the tax payable?
Ans – Since it is a Direct Tax proposal it will normally be applicable for the Assessment Year FY19-20 (Financial Year FY18-19). In other words, the LT Capital gains, of over Rs 1 Lakh, made for the year FY18-19 will be liable to tax at 10%.
3. Does it mean that there is no LTCG for Assessment Year FY18-19 (Financial Year FY17-18)?
Ans – One needs to understand the exact proposal in fine print. However, it appears that any LTCG will not be applicable for FY18-19 on plain read. This question frankly needs greater degree of expert study.
4. What is the relevance of the cut-off date of 31st Jan 2018?
Ans – The FM has proposed grandfathering of LT Capital gains upto 31st Jan 2018. Any incremental LT Capital gains after that will be counted as LT Capital gains for the new tax.
5. What happens to my tax liability if I sell stocks starting today held for more than a year?
Ans – As for LT Capital gains made in Financial Year 17-18 (i.e sale upto 31st Mar 2018), it appears there is no tax. However, any sale made after 1st April 2018 will be liable to the new LTCG tax. One needs to segregate this LT capital gain into two parts
a) Part one – is LT Capital gains made upto 31st Jan 2018. This will be highest price of the stock on 31st Jan 2018 minus the cost of acquiring stock;
b) Part two – is LT Capital gains made after 31st Jan 2018. This will be sale price minus highest price of the stock on 31st Jan 2018.
While Part one will be exempt. It is the Part two that will be assessed as LT Capital gains (it can also be a Capital loss) for Tax. Tax on this will be computed at the rate of 10% (+ cess of 3%) only if exceeds Rs 1 Lakh
6. What should be the strategy now on equity investments?
Ans – Any equity investor wishing to reduce the LT Capital gains tax liability can sell stocks starting today till 31st March 2018 and incur zero tax provided the holding period is more than a year. However, one can continue to buy equity shares without any hesitation. Any future sales after 31st March 2018 has to be judiciously chosen to minimize the tax liability. Assuming equity investments yield a return of 15% every year, an investment of Rs6.66L each year will rise to Rs7.66L in a year and gains booked thereof will be tax free. Even if the gains exceed 15% to say 25%, the LT gains Tax will be Rs6,667/- only
Long Term Capital Gains Tax – FAQs
1. What is the budget proposal on LTCG for equities?
Ans – So far, any LT Capital gains made on equities on Exchanges was exempt. The Govt has now proposed an 10% LTCG tax on gains made above Rs 1 Lakh
2. When is the tax payable?
Ans – Since it is a Direct Tax proposal it will normally be applicable for the Assessment Year FY19-20 (Financial Year FY18-19). In other words, the LT Capital gains, of over Rs 1 Lakh, made for the year FY18-19 will be liable to tax at 10%.
3. Does it mean that there is no LTCG for Assessment Year FY18-19 (Financial Year FY17-18)?
Ans – One needs to understand the exact proposal in fine print. However, it appears that any LTCG will not be applicable for FY18-19 on plain read. This question frankly needs greater degree of expert study.
4. What is the relevance of the cut-off date of 31st Jan 2018?
Ans – The FM has proposed grandfathering of LT Capital gains upto 31st Jan 2018. Any incremental LT Capital gains after that will be counted as LT Capital gains for the new tax.
5. What happens to my tax liability if I sell stocks starting today held for more than a year?
Ans – As for LT Capital gains made in Financial Year 17-18 (i.e sale upto 31st Mar 2018), it appears there is no tax. However, any sale made after 1st April 2018 will be liable to the new LTCG tax. One needs to segregate this LT capital gain into two parts
a) Part one – is LT Capital gains made upto 31st Jan 2018. This will be highest price of the stock on 31st Jan 2018 minus the cost of acquiring stock;
b) Part two – is LT Capital gains made after 31st Jan 2018. This will be sale price minus highest price of the stock on 31st Jan 2018.
While Part one will be exempt. It is the Part two that will be assessed as LT Capital gains (it can also be a Capital loss) for Tax. Tax on this will be computed at the rate of 10% (+ cess of 3%) only if exceeds Rs 1 Lakh
6. What should be the strategy now on equity investments?
Ans – Any equity investor wishing to reduce the LT Capital gains tax liability can sell stocks starting today till 31st March 2018 and incur zero tax provided the holding period is more than a year. However, one can continue to buy equity shares without any hesitation. Any future sales after 31st March 2018 has to be judiciously chosen to minimize the tax liability. Assuming equity investments yield a return of 15% every year, an investment of Rs6.66L each year will rise to Rs7.66L in a year and gains booked thereof will be tax free. Even if the gains exceed 15% to say 25%, the LT gains Tax will be Rs6,667/- only
Saturday, January 27, 2018
Lenovo android phone not visible on android studio
My Lenovo K6 power was not visible on device chooser window. I did enable the developer option and usb debugging option. Even after that my phone was not visible on Android studio device chooser window. Then finally I followed following link and it worked :
https://lenovomobilesupport.lenovo.com/in/en/solutions/ht502856
https://lenovomobilesupport.lenovo.com/in/en/solutions/ht502856
Subscribe to:
Posts (Atom)